
Zusammenfassung Bachelor Thesis mit dem Thema:
Multikriterielle ein-zu-viele-Suche nach pareto-optimalen Pfaden im zeitabhängigen Graphen
03.11.17 von Benedikt Naumann
In Rahmen meiner Bachelorthesis habe ich ein Projekt der Algorithmik Gruppe des Fachbereichs Informatik der TU Darmstadt um bestimmte Funktionalitäten erweitert.
Dieses Forschungsprojekt versucht einen alternativen Ansatz zum Finden von Bahnverbindungen zu realisieren. Die Neuerung hierbei ist, dass der zugrundeliegende Algorithmus, welcher die optimale Verbindung zwischen zwei Haltestellen heraussucht, in der Lage ist, mehrere Kriterien bei der Suche zu berücksichtigen, um dann alle, nach den gegebenen Kriterien, optimalen Verbindungen, zu finden.
Dies macht das Problem der optimalen Verbindungen deutlich komplexer, denn während es bei den klassischen Ansätzen jeweils nur eine optimale Verbindung geben kann, ändert sich dies, wenn man mehrere Kriterien in der Suche zulässt.
Deutlich wird dies, wenn man sich folgenden Fall ansieht:
Verbindung A Dauert 30 Minuten und kostet 10€
Verbindung B Dauert 20 Minuten und kostet 15€
Nach dem klassischen Ansatz würde man einfach Verbindung B als Ergebnis liefern, denn diese ist eindeutig schneller. Wenn man nun jedoch sowohl die Fahrtzeit als auch die Kosten berücksichtig, sind beide Verbindungen optimal. Denn keine Verbindung ist in allen Kriterien besser oder gleich gut wie die andere.
Um diesen gesteigerten Anforderungen gerecht zu werden, wurde ausgehen vom Standard-Algorithmus für solche Probleme eine modifizierte Variante dieses Algorithmus entwickelt. Der Standard-Algorithmus heißt Dijkstras-kürzester-Pfad Algorithmus, oder auch kurz Dijkstras Algorithmus. Dieser, schon 1956 entdeckte Algorithmus, wird auch heute noch in seiner reinen oder modifizierten Varianten von den meisten Routenfindern verwendet.
Prominente Beispiele sind Google Maps, TomTom oder der Routenplaner der Deutschen Bahn.
Allerdings kann dieser Algorithmus nicht trivial für das optimieren nach mehreren Kriterien erweitert werden.
Aus diesem Grund wurde von der Algorithmik Forschungsgruppe der sogenannte Pareto-Dijkstra Algorithmus entwickelt. Dieser ist deutlich komplexer als der normale Dijkstra und Ansatzpunkt meiner Thesis.
Die Aufgabe meiner Thesis war es nun, den pareto-dijkstra Algorithmus so zu erweitern, dass er in der Lage ist, diese Suche von einem Startpunkt, zu einer Startzeit, zu beliebig vielen Zielen die optimale Verbindung zu finden. Diese Art der Suche nennt man im Allgemeinen „ein-zu-viele Suche“ oder auch kurz 1:N. Neben der Korrektheit der Ergebnisse, war vor allem die Geschwindigkeit der Suche entscheidend.
Um nun die 1:N Suche möglichst schnell zu bekommen, evaluierte ich zwei verschiedene Ansätze.
Der erste war die schon existierende Suche einfach für jedes Ziel einmal anzuwenden.
Das heißt, dass der Algorithmus alle Ziele nimmt und die Suche für jedes Ziel neu startet und sie anschließend geschlossen in einer Ausgabe zurückgibt.
Dieser Ansatz funktionierte zwar insofern, dass die Ergebnisse korrekt waren, jedoch war die Geschwindigkeit nicht zufriedenstellend. Denn mit steigender Zahl an Zielen, stieg die Laufzeit linear mit.
Das Bedeutet, dass eine Verdoppelung der Ziele eine Verdopplung der Laufzeit mit sich brachte.
Um nun die Laufzeit zu verbessern musste ich Modifikationen an dem verwendeten Suchalgorithmus vornehmen. Die Idee hinter den Änderungen war, den Algorithmus nach allen gegebenen Zielen gleichzeitig Suchen zu lassen. Dies ermöglichte es Synergieeffekte auszunutzen.
Man kann sich diese so vorstellen, dass wenn z.B. zwei Ziele nah beieinander sind, die Fahrt zu diesen Zielen größtenteils gleich ist. Wenn man nun also nach Verbindungen beider dieser Ziele gleichzeitig sucht, muss man die entsprechenden Verbindungen, die sich überschneiden, nur einmal heraussuchen und hat somit Zeit gespart.
Durch die von mir eingeführten Änderungen ist die Laufzeit, vor allem für sehr viele Ziele, deutlich nach unten gegangen. Um die Laufzeit noch weiter zu drücken, habe ich im Anschluss die eben vorgestellten Ansätze parallelisiert. Das Bedeutet, dass ich die Algorithmen so modifiziert habe, dass diese auf mehreren CPU-Kernen gleichzeitig ausgeführt werden können. Dies führte zu einem weiteren Geschwindigkeitsanstieg.
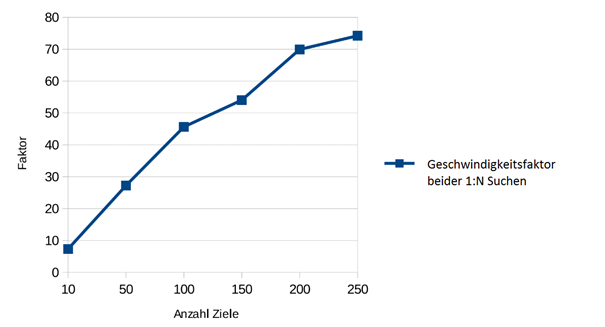
Insgesamt ist es mir in meiner Thesis gelungen einen Algorithmus zu entwickeln, der im Vergleich zu dem trivialen sequenziellen Ansatz, deutlich schneller ist. So ist man schon mit einer Anzahl von 15 Zielen um den Faktor 10 und bei 250 Zielen um den Faktor 75 schneller als in der sequenziellen Suche.
Zusammenfassend hat mich das Arbeiten an meiner Thesis sehr gefordert
aber auch viel Spaß gemacht hat.
Ich konnte viel von meinem im Studium gelernten Wissen verwenden, musste mich aber auch in ein neues Problemfeld einarbeiten. Dazu musste ich dieses nicht nur verstehen sondern auch um neue Ideen und Ansätze erweitern. Sowohl der Praktische als auch der theoretische Anspruch waren sowohl sehr interessant als auch fordernd. So musste ich mir nicht nur durch das Einlesen in verschiedene aktuelle Forschungsarbeiten das Wissen über das Problemfeld aneignen, sondern hatte auch mit praktischen Programmierproblemen, wie etwa der parallelen Programmierung, zu tun.
Abschließend kann man sagen, dass meine Bachelorthesis einen guten vertiefenden Charakter zum Abschluss meiner Bachelorstudiums hatte und die darin erworbenen Fähigkeiten mir in meiner weiteren Laufbahn viel nutzen werden.
